ฟังก์ชัน SIN Excel เป็นฟังก์ชันตรีโกณมิติแบบ inbuilt ใน excel ซึ่งใช้ในการคำนวณค่าไซน์ของจำนวนที่กำหนดหรือในแง่ของตรีโกณมิติค่าไซน์ของมุมที่กำหนดมุมนี้เป็นตัวเลขใน excel และฟังก์ชันนี้ใช้เพียงอาร์กิวเมนต์เดียว ซึ่งเป็นหมายเลขอินพุตที่ระบุ

ฟังก์ชัน SIN ใน Excel

ฟังก์ชัน SIN ใน Excel คำนวณไซน์ของมุมที่เราระบุ ฟังก์ชัน SIN ใน Excel ถูกจัดประเภทเป็นฟังก์ชันคณิตศาสตร์ / ตรีโกณมิติใน Excel SIN ใน excel จะส่งกลับค่าตัวเลขเสมอ

ในคณิตศาสตร์และตรีโกณมิติ SINE เป็นฟังก์ชันตรีโกณมิติของมุมซึ่งในรูปสามเหลี่ยมมุมฉากจะเท่ากับความยาวของด้านตรงข้าม (ด้านที่ทำมุมฉาก) หารด้วยความยาวของด้านตรงข้ามมุมฉากและแสดงเป็น :

Sin Θ = ด้านตรงข้าม / ด้านตรงข้ามมุมฉาก

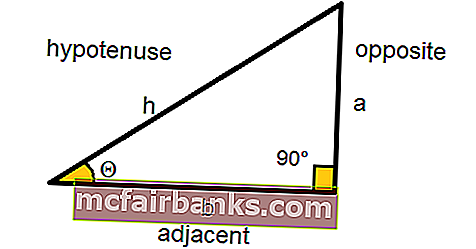
บาปΘ = a / h

สูตร SIN ใน Excel

ด้านล่างนี้คือสูตร SIN ใน Excel

โดยที่ number คืออาร์กิวเมนต์ที่ส่งไปยังสูตร SIN ในหน่วยเรเดียน

ถ้าเราส่งมุมไปที่ SIN โดยตรงในฟังก์ชัน excel มันจะไม่รับรู้ว่ามันเป็นอาร์กิวเมนต์ที่ถูกต้อง ตัวอย่างเช่นถ้าเราส่ง 30 °เป็นอาร์กิวเมนต์ไปยังฟังก์ชัน SIN นี้ใน Excel จะไม่รับรู้ว่าเป็นอาร์กิวเมนต์ที่ถูกต้อง Excel จะแสดงข้อความแสดงข้อผิดพลาด

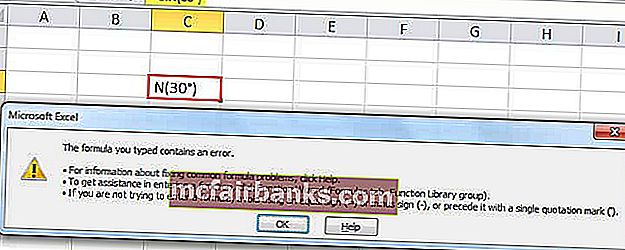
ดังนั้นอาร์กิวเมนต์ที่เราต้องผ่านต้องเป็นเรเดียน

ในการแปลงมุมเป็นเรเดียนมีสองวิธี

1. ใช้ฟังก์ชัน Excel RADIANS ในตัว ฟังก์ชัน RADIANS จะแปลงองศาเป็นค่าเรเดียน

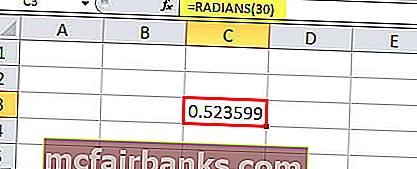
ตัวอย่างเช่นในการแปลง 30 °เป็นเรเดียนเราจะใช้ฟังก์ชันนี้โดยใช้องศาเป็นตัวเลขมันจะ 30 °เป็น 30

= RADIANS (30)จะให้เรเดียน 0.52

2. ในกรณีที่สองเราสามารถใช้สูตรทางคณิตศาสตร์สำหรับการแปลงองศาเป็นเรเดียน สูตรคือ

เรเดียน = องศา * (π / 180) (π = 3.14)

ใน excel ยังมีฟังก์ชันที่ส่งกลับค่า Pi ที่ถูกต้องถึง 15 หลักและฟังก์ชันคือPI ()

ดังนั้นสำหรับการแปลงองศาเป็นเรเดียนเราจะใช้สูตร

เรเดียน = องศา * (PI () / 180)

วิธีใช้ฟังก์ชัน SIN ใน Excel

ฟังก์ชัน SIN ใน Excel นั้นง่ายมากและใช้งานง่าย ให้ทำความเข้าใจการทำงานของ SIN ใน excel ตามตัวอย่าง

คุณสามารถดาวน์โหลด SIN นี้ในเทมเพลต Excel ได้ที่นี่ - SIN ในเทมเพลต Excel

SIN ใน Excel ตัวอย่าง # 1

การคำนวณค่าไซน์โดยใช้ฟังก์ชัน SIN ใน Excel และฟังก์ชัน RADIANS ใน Excel

การคำนวณค่าไซน์โดยใช้ฟังก์ชัน SIN ใน Excel และฟังก์ชัน PI

ฟังก์ชันไซน์ใน Excel มีแอปพลิเคชันในชีวิตจริงมากมาย มีการใช้กันอย่างแพร่หลายในสถาปัตยกรรมเพื่อคำนวณความสูงและความยาวของรูปทรงเรขาคณิต นอกจากนี้ยังใช้ใน GPS, ทัศนศาสตร์, การคำนวณวิถี, เพื่อค้นหาเส้นทางที่สั้นที่สุดตามตำแหน่งทางภูมิศาสตร์ละติจูดและลองจิจูดวิทยุกระจายเสียง ฯลฯ แม้แต่คลื่นแม่เหล็กไฟฟ้าก็ถูกพล็อตเป็นกราฟของฟังก์ชันไซน์และโคไซน์

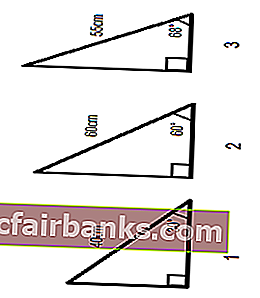
สมมติว่าเรามีสามเหลี่ยมมุมฉากสามรูปโดยพิจารณาจากมุมและความยาวของด้านหนึ่งและเราต้องคำนวณความยาวของอีกสองด้าน

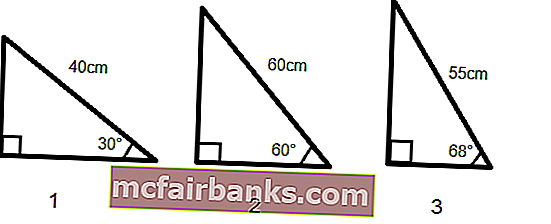
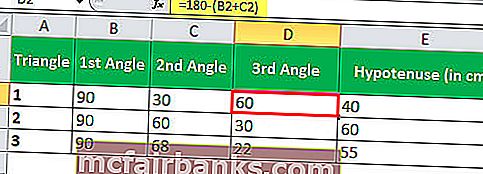
ผลรวมของมุมทั้งหมดบนสามเหลี่ยมเท่ากับ 180 °ดังนั้นเราจึงคำนวณมุมที่สามได้อย่างง่ายดาย

เรารู้ว่า Sin Θ = ตรงกันข้าม / ด้านตรงข้ามมุมฉาก

ดังนั้นความยาวด้านตรงข้ามจะเป็นSin Θ * ด้านตรงข้ามมุมฉาก

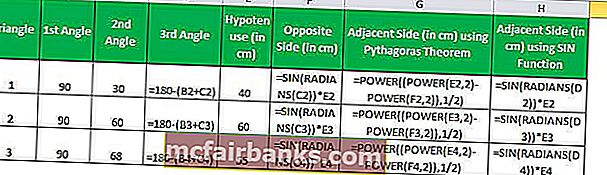
ใน Excel ความยาวของด้านตรงข้าม (ด้านตั้งฉาก) จะคำนวณโดยสูตร SIN

= SIN (เรเดียน (C2)) * E2

ใช้สูตร SIN ที่ให้ไว้ข้างต้นสำหรับสามเหลี่ยมสามรูปเราจะได้ความยาวของสามเหลี่ยมตั้งฉาก

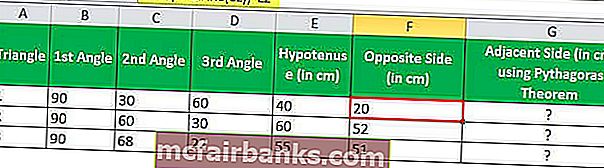
สำหรับด้านที่สาม (ด้านติดกัน) เรามีสองวิธี - โดยใช้ทฤษฎีบทพีทาโกรัสหรืออีกครั้งโดยใช้ฟังก์ชัน SIN ใน Excel จากมุมอื่น ๆ

ตามทฤษฎีบทของพีทาโกรัสผลรวมของกำลังสองของด้านสองด้านของสามเหลี่ยมมุมฉากจะเทียบเท่ากับกำลังสองของด้านตรงข้ามมุมฉาก

Hypotenuse2 = ตรงข้าม 2 + ติดกัน 2

ที่อยู่ติดกัน = (Hypotenuse2 - Opposite2) 1/2

ใน excel เราจะเขียนเป็น

= POWER ((POWER (ด้านตรงข้าม, 2) -POWER (ตรงข้าม, 2)), 1/2)

ใช้สูตรนี้คำนวณความยาวของด้านที่อยู่ติดกัน

= พลังงาน ((POWER (E2,2) -POWER (F2,2)), 1/2)

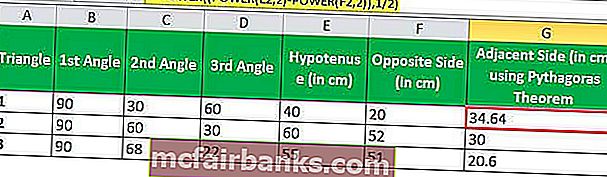
ด้วยวิธีที่สองเราสามารถใช้ SINE ของมุมที่ 3 เพื่อคำนวณค่าของด้านที่อยู่ติดกัน

ถ้าเราหมุนสามเหลี่ยมไปทางซ้าย 90 °ด้านตรงข้ามจะสลับกับด้านที่อยู่ติดกันและ SIN ของมุมระหว่างด้านตรงข้ามมุมฉากและด้านที่อยู่ติดกันจะช่วยในการคำนวณค่าของด้านที่สาม

= SIN (เรเดียน (D2)) * E2

SIN ใน Excel ตัวอย่าง # 2

มีอาคารสูงที่ไม่ทราบความสูงและ Sun ray ณ จุดหนึ่งทำมุมที่จุด A ที่ 75 °จึงทำให้เงาของอาคารยาว 70 เมตร เราจำเป็นต้องหาความสูงของหอคอย

ความสูงของอาคารจะคำนวณโดยใช้ฟังก์ชัน SIN ใน excel

SIN 75 ° = ความสูงของสิ่งปลูกสร้าง / ความยาวของเงาที่จุด A

ดังนั้นความสูงของอาคาร = SIN 75 ° * ความยาวของเงาที่จุด A

ดังนั้นความสูงของอาคารจะเป็น

= SIN (เรเดียน (B3)) * B2

ความสูงของอาคาร 67.61 เมตร

SIN ใน Excel ตัวอย่าง # 3

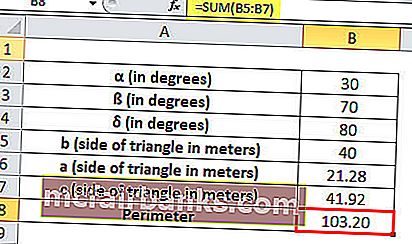
เรามีที่ดินในรูปสามเหลี่ยมซึ่งมุมทั้งสองจะได้รับเป็น 30 °และ 70 °และเรารู้เพียงความยาวของด้านหนึ่งของสามเหลี่ยมซึ่งเป็น 40 เมตร เราต้องหาความยาวของด้านอื่น ๆ อีกสามด้านและเส้นรอบวงของสามเหลี่ยม

สำหรับรูปสามเหลี่ยมเมื่อทราบด้านหนึ่งและมุมทั้งหมดเราสามารถคำนวณด้านอื่น ๆ ได้โดยใช้กฎไซน์

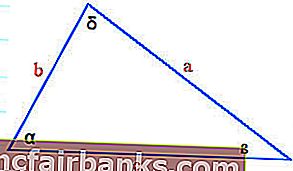
กฎไซน์ในตรีโกณมิติให้ความสัมพันธ์ของมุมบาปและด้านข้างของสามเหลี่ยมด้วยสูตร SIN

a / sin α = b / sin ß = c / sin δ

ในกรณีนี้,

α = 30 °, ß = 70 °และδ = 180 ° - (30 ° + 70 °) = 80 °และด้านหนึ่งของสามเหลี่ยม b = 40 เมตร

ในการค้นหาด้านอื่น ๆ ของสามเหลี่ยมเราจะใช้กฎไซน์

a = บาปα * (b / sin ß)

ดังนั้น,

a = SIN (เรเดียน (30)) * (B5 / SIN (เรเดียน (70)))

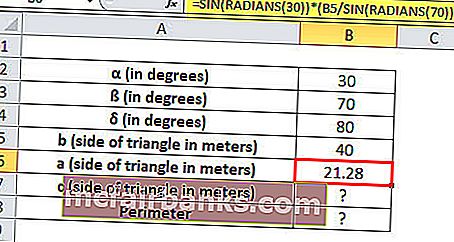
ความยาวด้าน a = 21.28 เมตร

ในทำนองเดียวกันด้านที่สาม c จะเป็น

c = บาปδ * (b / sin ß)

ดังนั้น,

c = SIN (เรเดียน (80)) * (B5 / SIN (เรเดียน (70)))

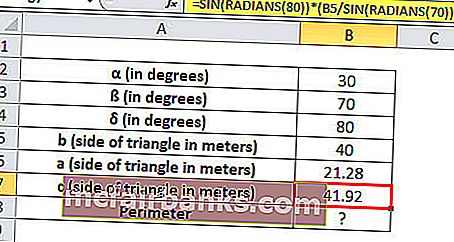
ด้านทั้งสามของสามเหลี่ยมมีความยาว 21.28, 40, 41.92 เมตร

ปริมณฑลของสามเหลี่ยมคือผลรวมของด้านทั้งหมด

ดังนั้นเส้นรอบวงจะเป็น= SUM (B5: B7)